In the previous post, I described how to use a neural net to learn an operator, whose form was explicit. In this post, I am going to try and learn the operator \(L\), and hence the operator \(L^T\) as well, since we can't compute it explicitly this time.
While the ROF model is efficient for denoising, its form is hand crafted, and one might wonder if there might be a more optimal formulation for this problem. Since the Primal Dual Framework works for a more general set of problems, i.e.:
$$ \begin{align} & \underset{x}{\text{minimize}} & & M(x) + R(Lx) \end{align} $$ with:
- \(M\) a lower semi continuous function
- \(R\) a lower semi continuous function
- \(L\) a continuous linear operator
we are going to explore in this post the possibility of learning these functions \(M\), \(R\)and \(L\), as well as the parameters \( \tau\), \( \sigma\) and \( \theta \) through a neural net with the observed images as input and the ground truth images as outputs. The layers will be custom layers consisting of the parametrized Primal Dual steps. The goal will be to optimize these parameters.
The idea here is a bit similar to the OptNet paper.
A more general formulation of the ROF model
But first, let's begin by giving a more general formulation of the ROF model: $$ \begin{align} & \underset{x}{\text{minimize}} & & \frac{1}{2} x^T H x + b^T x + \left\| Lx \right\|_1 \end{align} $$ with:
- \(H\) a symmetric invertible matrix of \(\mathcal{M}_n(\mathbb{R}^n\))
- \(b\) is a vector in \(\mathbb{R}^n\)
- \(L\) is a continuous linear operator
Let's now use the following characterization of a norm : \(\left\| Lx \right\|_1 = \underset{y \in [-1, 1]^n}{\max}\langle L^T y, x \rangle\) in order to introduce a saddle problem formulation. The problem can now be written: $$ \begin{align} & \underset{x}{\min} \underset{y \in [-1, 1]^n }{\max}& & \frac{1}{2} x^T H x + \langle b + L^T y, x \rangle \end{align} $$ A simple gradient computation gives: \(x^* = -H^{-1} (b + L^T y) \). The dual problem is then: $$ \begin{align} & \underset{y \in [-1, 1]^n}{\text{maximize}} & & -\frac{1}{2} (b+L^T y )^T H^{-1} (b+L^Ty) \end{align} $$ We are going to note this function to maximize \(D(y; H, b, L)\).
The primal-dual gap is defined as : \(G(x, y ; H, b, L) = P(x; H, b, L) - D(y; H, b, L)\). Since this is a saddle point problem, we have that \(G(x^*, y^* ; H, b, L) = G(x^* ; H, b, L) = 0 \)
Now, we are going to consider this optimization problem through a computational graph view. It looks very similar to the one in the excellent paper Learning to learn by gradient descent by gradient descent:
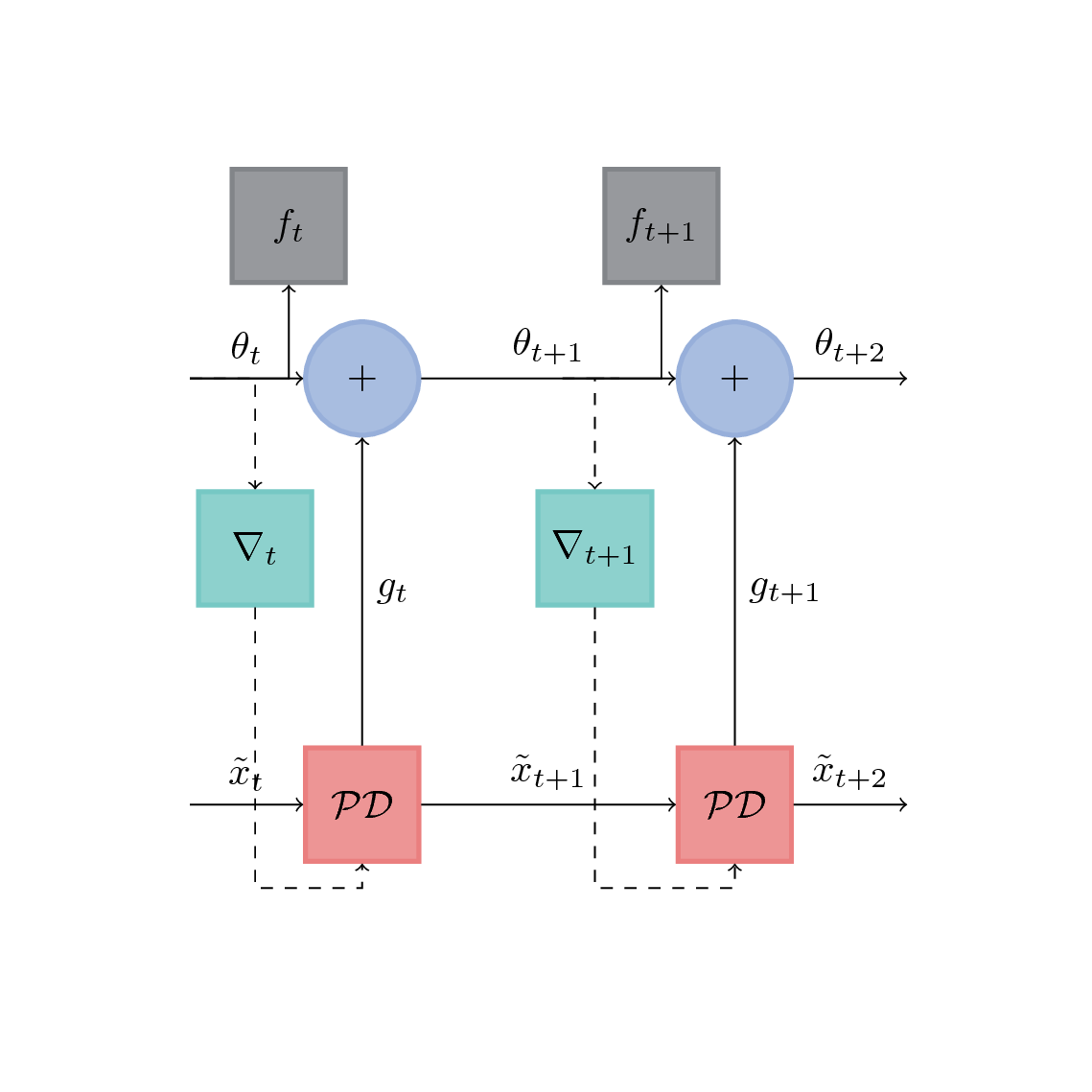
If we note \(\theta_t = (H, b, L)_t\) the vector of parameters that we are trying to learn in the Primal Dual problem, \(\mathcal{PD}\) the recurrent neural net that unrolls \(n\) iterations of the Primal Dual algorithm, \(\tilde{x}_t\) the primal variable after \(nk\) iterations, \(k \in \mathbb{N}\).
Let's start by learning a simple linear operator
Formulation of the simplified problem
In the previous general model, if we pose \( H = I_n \), \( b = -2 img_{obs}\) and \(L : x \mapsto \sum_{(i, j) \in \mathcal{E}} \|x_i -x_j \|_1\), we can get back to the usual ROF model, as formulated in the Chambolle Pock paper: $$ \begin{align} & \underset{x}{\text{minimize}} & & \| x - img_{obs} \|_2^2 + \frac{\lambda}{2} \left\| Lx \right\|_1 \end{align} $$ Since this model has been studied in the previous blog post, we are going to introduce the linear operator \(L : x ; w \mapsto \sum_{(i, j) \in \mathcal{E}} w_{i,j} \|x_i -x_j \|_1\), i.e \(L = W \odot \nabla\), \(\odot \) being the Hadamard product here. A calculation shows that \(L\) is a linear operator, and that its adjoint \(L^T\) is \( L^T : y \mapsto - div(W \odot y) \).
Now let's talk a little bit about the form of the matrix \(W = (w_{i,j})_{ij} \); the operator \(L \) is supposed to be learning for any image that we take as an input for our algorithm. So if neighboring pixels have a very high absolute difference in one image, a new independant image is very unlikely to have the same high differences at the same locations in the images. This leads to the intuition that \(\forall (i, j), \ (w_{i,j})_{ij} \simeq c \). So we are going to pose : \(\forall (i, j), \ \mathbb{w}_{i,j} = \lambda_1 + \lambda_2 \exp (- L(x_i, x_j; \mathbb{w}) \), and try and learn the parameters \(\theta = (\lambda_1 , \lambda_2, \mathbb{w}) \). Since our output here is structured, and that \(L\) is the pairwise operator in our problem formulation, it would be interesting to try and to learn \( \mathbb{w} \) with a couple of convolutional layers in the neural net.
Here is a view of what the neural net looks like:
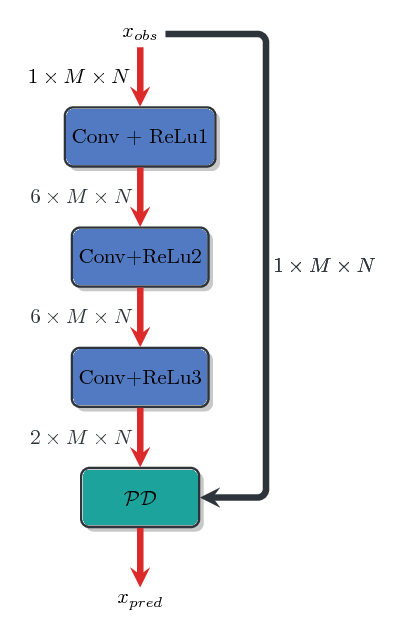
An example
As a first example, I want to test this approach on a dozen different images, with an additive Gaussian noise with zero mean and a standard deviation that we set arbitrarily to \( 0.1 \), for each image. Then, each image is selected randomly in the list of images in the dataset, and noised with a Gaussian noise with the previous standard deviation.
In this scenario, I am going to minimize the Mean Squared Error between the Ground Truth and the primal variable after \( n\) iterations of the primal dual algorithm: $$ \begin{align} & \underset{w}{\text{minimize}} & & \sum{\left\| x_i^{*} - x_i^{GT} \right\|_2^2 } \\ & ST & & x_i^{*} = \underset{x}{\arg \min P(x; w)} \end{align} $$ Each function was optimized for 100 steps and the Primal-Dual net was unrolled for 20 steps, during 10 epochs. The parameters \(\sigma, \lambda_{ROF}, \theta, \tau \) were also learned in the process. I chose a fixed \(sigma_{noise} = 0.07 \) in order to compare the results with denoising benchmarks.
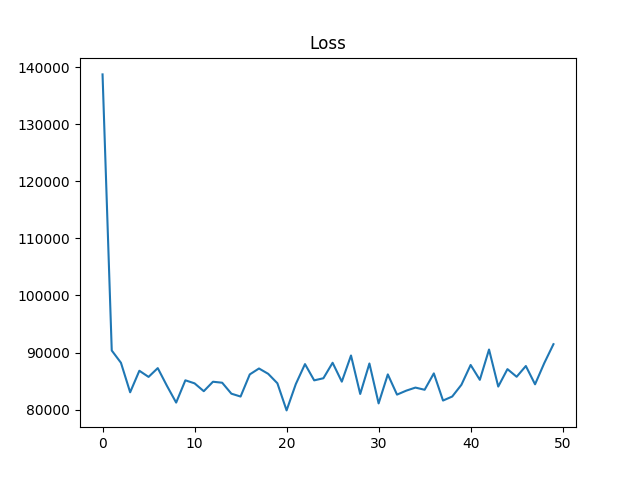



Here are other examples from the data set, with \( \sigma = 0.07\):









It seems to denoise pretty nicely, even with a strong noise in the observed image. The average running time in the testing setup in \(0.06\) seconds.
Python Code Example with PyTorch
Here is how I organized the code with PyTorch, with GPU support. Every function needed in the Primal Dual Net is coded as a nn.Module submodule:
from torch.autograd import Variable
import torch
import torch.nn as nn
class ForwardWeightedGradient(nn.Module):
def __init__(self):
super(ForwardWeightedGradient, self).__init__()
def forward(self, x, w, dtype=torch.cuda.FloatTensor):
"""
:param x: PyTorch Variable [1xMxN]
:param w: PyTorch Variable [2xMxN]
:param dtype: Tensor type
:return: PyTorch Variable [2xMxN]
"""
im_size = x.size()
gradient = Variable(torch.zeros((2, im_size[1], im_size[2])).type(dtype)) # Allocate gradient array
# Horizontal direction
gradient[0, :, :-1] = x[0, :, 1:] - x[0, :, :-1]
# Vertical direction
gradient[1, :-1, :] = x[0, 1:, :] - x[0, :-1, :]
gradient = gradient * w
return gradient
class BackwardWeightedDivergence(nn.Module):
def __init__(self):
super(BackwardWeightedDivergence, self).__init__()
def forward(self, y, w, dtype=torch.cuda.FloatTensor):
"""
:param y: PyTorch Variable, [2xMxN], dual variable
:param dtype: tensor type
:return: PyTorch Variable, [1xMxN], divergence
"""
im_size = y.size()
y_w = w.cuda() * y
# Horizontal direction
d_h = Variable(torch.zeros((1, im_size[1], im_size[2])).type(dtype))
d_h[0, :, 0] = y_w[0, :, 0]
d_h[0, :, 1:-1] = y_w[0, :, 1:-1] - y_w[0, :, :-2]
d_h[0, :, -1] = -y_w[0, :, -2:-1]
# Vertical direction
d_v = Variable(torch.zeros((1, im_size[1], im_size[2])).type(dtype))
d_v[0, 0, :] = y_w[1, 0, :]
d_v[0, 1:-1, :] = y_w[1, 1:-1, :] - y_w[1, :-2, :]
d_v[0, -1, :] = -y_w[1, -2:-1, :]
# Divergence
div = d_h + d_v
return div
class PrimalWeightedUpdate(nn.Module):
def __init__(self, lambda_rof, tau):
super(PrimalWeightedUpdate, self).__init__()
self.backward_div = BackwardWeightedDivergence()
self.tau = tau
self.lambda_rof = lambda_rof
def forward(self, x, y, img_obs, w):
"""
:param x: PyTorch Variable [1xMxN]
:param y: PyTorch Variable [2xMxN]
:param img_obs: PyTorch Variable [1xMxN]
:return:Pytorch Variable, [1xMxN]
"""
x = (x + self.tau * self.backward_div.forward(y, w) +
self.lambda_rof * self.tau * img_obs) / (1.0 + self.lambda_rof * self.tau)
return x
class DualWeightedUpdate(nn.Module):
def __init__(self, sigma):
super(DualWeightedUpdate, self).__init__()
self.forward_grad = ForwardWeightedGradient()
self.sigma = sigma
def forward(self, x_tilde, y, w):
"""
:param x_tilde: PyTorch Variable, [1xMxN]
:param y: PyTorch Variable, [2xMxN]
:param w: PyTorch Variable, [2xMxN]
:return: PyTorch Variable, [2xMxN]
"""
y = y + self.sigma * self.forward_grad.forward(x_tilde, w)
return y
class PrimalRegularization(nn.Module):
def __init__(self, theta):
super(PrimalRegularization, self).__init__()
self.theta = theta
def forward(self, x, x_tilde, x_old):
"""
:param x: PyTorch Variable, [1xMxN]
:param x_tilde: PyTorch Variable, [1xMxN]
:param x_old: PyTorch Variable, [1xMxN]
:return: PyTorch Variable, [1xMxN]
"""
x_tilde = x + self.theta * (x - x_old)
return x_tilde
class LinearOperator(nn.Module):
"""
Neural Layers to learn the linear operator L.
"""
def __init__(self):
super(LinearOperator, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=3, stride=1, padding=1).cuda()
self.conv2 = nn.Conv2d(10, 10, kernel_size=3, stride=1, padding=1).cuda()
self.conv3 = nn.Conv2d(10, 2, kernel_size=3, stride=1, padding=1).cuda()
def forward(self, x):
"""
:param x:
:return:
"""
z = Variable(x.data.unsqueeze(0)).cuda()
z = F.relu(self.conv1(z))
z = F.relu(self.conv2(z))
z = F.relu(self.conv3(z))
y = Variable(z.data.squeeze(0).cuda())
return y
class GaussianNoiseGenerator(nn.Module):
"""
Gaussian noise generator for an image.
"""
def __init__(self):
super(GaussianNoiseGenerator, self).__init__()
def forward(self, img, std, mean=0.0, dtype=torch.cuda.FloatTensor):
"""
:param img:
:param std:
:param mean:
:param dtype:
:return:
"""
noise = torch.zeros(img.size()).type(dtype)
noise.normal_(mean, std=std)
img_n = img + noise
return img_n
class Net(nn.Module):
def __init__(self, w1, w2, w, max_it, lambda_rof, sigma, tau, theta, dtype=torch.cuda.FloatTensor):
super(Net, self).__init__()
self.linear_op = LinearOperator()
self.max_it = max_it
self.dual_update = DualWeightedUpdate(sigma)
self.prox_l_inf = ProximalLinfBall()
self.primal_update = PrimalWeightedUpdate(lambda_rof, tau)
self.primal_reg = PrimalRegularization(theta)
self.pe = 0.0
self.de = 0.0
self.w1 = nn.Parameter(w1)
self.w2 = nn.Parameter(w2)
self.w = w
self.clambda = nn.Parameter(lambda_rof.data)
self.sigma = nn.Parameter(sigma.data)
self.tau = nn.Parameter(tau.data)
self.theta = nn.Parameter(theta.data)
self.type = dtype
def forward(self, x, img_obs):
"""
:param x:
:param img_obs:
:return:
"""
x = Variable(img_obs.data.clone()).cuda()
x_tilde = Variable(img_obs.data.clone()).cuda()
img_size = img_obs.size()
y = Variable(torch.ones((img_size[0] + 1, img_size[1], img_size[2]))).cuda()
# Forward pass
y = self.linear_op(x)
w_term = Variable(torch.exp(-torch.abs(y.data.expand_as(y))))
self.w = self.w1.expand_as(y) + self.w2.expand_as(y) * w_term
self.w.type(self.type)
self.theta.data.clamp_(0, 5)
for it in range(self.max_it):
# Dual update
y = self.dual_update.forward(x_tilde, y, self.w)
y.data.clamp_(0, 1)
y = self.prox_l_inf.forward(y, 1.0)
# Primal update
x_old = x
x = self.primal_update.forward(x, y, img_obs, self.w)
x.data.clamp_(0, 1)
# Smoothing
x_tilde = self.primal_reg.forward(x, x_tilde, x_old)
x_tilde.data.clamp_(0, 1)
return x_tilde
And now here is what the training script looks like:
import argparse
import random
import string
import os
import glob
import numpy as np
import matplotlib.pyplot as plt
import png
from PIL import Image
import torch
from torch.autograd import Variable
from torch.utils.data import DataLoader
from torchvision import transforms
import torch.nn as nn
from data_io import NonNoisyImages
from linear_operators import ForwardGradient, ForwardWeightedGradient
from primal_dual_models import Net, GaussianNoiseGenerator
def id_generator(size=6, chars=string.ascii_letters + string.digits):
return ''.join(random.choice(chars) for _ in range(size))
def compute_mean_std_data(filelist):
"""
:param filelist:
:return:
"""
tensor_list = []
for file in filelist:
img = Image.open(file)
img_np = np.array(img).ravel()
tensor_list.append(img_np.ravel())
pixels = np.concatenate(tensor_list, axis=0)
return np.mean(pixels), np.std(pixels)
parser = argparse.ArgumentParser(description='Run Primal Dual Net.')
parser.add_argument('--use_cuda', type=bool, default=True,
help='Flag to use CUDA, if available')
parser.add_argument('--max_it', type=int, default=20,
help='Number of iterations in the Primal Dual algorithm')
parser.add_argument('--max_epochs', type=int, default=5000,
help='Number of epochs in the Primal Dual Net')
parser.add_argument('--lambda_rof', type=float, default=5.,
help='Step parameter in the ROF model')
parser.add_argument('--theta', type=int, default=0.9,
help='Regularization parameter in the Primal Dual algorithm')
parser.add_argument('--tau', type=int, default=0.01,
help='Step Parameter in Primal')
parser.add_argument('--save_flag', type=bool, default=True,
help='Flag to save or not the result images')
parser.add_argument('--log', type=bool, help="Flag to log loss in tensorboard", default=False)
parser.add_argument('--out_folder', help="output folder for images",
default="guillaume_norm_20it_5k_epochs_15narrow_sigma_smooth_loss_lr_10-4/")
parser.add_argument('--clip', type=float, default=0.1,
help='Value of clip for gradient clipping')
args = parser.parse_args()
# Supplemental imports
if args.log:
from tensorboard import SummaryWriter
# Keep track of loss in tensorboard
writer = SummaryWriter()
# Set parameters:
max_epochs = args.max_epochs
max_it = args.max_it
lambda_rof = args.lambda_rof
theta = args.theta
tau = args.tau
#sigma = 1. / (lambda_rof * tau)
sigma = 15.0
batch_size = 8
m, std =122.11/255., 53.55/255.
print(m, std)
# Transform dataset
transformations = transforms.Compose([transforms.Scale((512, 512)), transforms.ToTensor()])
dd = NonNoisyImages("/home/louise/src/blog/pytorch_primal_dual/images/BM3D/", transform=transformations)
#m, std = compute_mean_std_dataset(dd.data)
dtype = torch.cuda.FloatTensor
train_loader = DataLoader(dd,
batch_size=batch_size,
num_workers=4)
m1, n1 = compute_mean_std_data(train_loader.dataset.filelist)
print("m = ", m)
print("s = ", std)
# set up primal and dual variables
img_obs = Variable(train_loader.dataset[0]) # Init img_obs with first image in the data set
x = Variable(img_obs.data.clone().type(dtype))
x_tilde = Variable(img_obs.data.clone().type(dtype))
img_size = img_obs.size()
y = Variable(torch.zeros((img_size[0] + 1, img_size[1], img_size[2])).type(dtype))
y = ForwardGradient().forward(x)
g_ref = y.clone()
# Net approach
w1 = 0.5 * torch.ones([1]).type(dtype)
w2 = 0.4 * torch.ones([1]).type(dtype)
w = Variable(torch.rand(y.size()).type(dtype))
# Primal dual parameters as net parameters
lambda_rof = nn.Parameter(lambda_rof * torch.ones([1]).type(dtype))
sigma = nn.Parameter(sigma * torch.ones([1]).type(dtype))
tau = nn.Parameter(tau * torch.ones([1]).type(dtype))
theta = nn.Parameter(theta*torch.ones([1]).type(dtype))
n_w = torch.norm(w, 2, dim=0)
plt.figure()
plt.imshow(n_w.data.cpu().numpy())
plt.colorbar()
plt.title("Norm of Initial Weights of Gradient of Noised image")
net = Net(w1, w2, w, max_it, lambda_rof, sigma, tau, theta)
criterion = torch.nn.MSELoss(size_average=True)
criterion_g = torch.nn.MSELoss(size_average=True)
optimizer = torch.optim.Adam(net.parameters(), lr=1e-4)
params = list(net.parameters())
loss_history = []
primal_history = []
dual_history = []
gap_history = []
it = 0
print(dd.filelist[0])
img_ref = Variable(train_loader.dataset[0]).type(dtype)
#std = 0.3 * torch.ones([1])
for t in range(max_epochs):
# Pick random image in dataset
img_ref = Variable(random.choice(train_loader.dataset)).type(dtype)
#print(img_ref)
y = ForwardGradient().forward(img_ref)
# Pick random noise variance in the given range
std = np.random.uniform(0.05, 0.1, 1)
# Apply noise on chosen image
img_obs = torch.clamp(GaussianNoiseGenerator().forward(img_ref.data, std[0]), min=0.0, max=1.0)
img_obs = Variable(img_obs).type(dtype)
x = Variable(img_obs.data.clone())
w = Variable(torch.rand(y.size()).type(dtype))
y = ForwardWeightedGradient().forward(x, w)
# Forward pass: Compute predicted image by passing x to the model
x_pred = net(x, img_obs)
# Compute and print loss
g_ref = Variable(ForwardWeightedGradient().forward(img_ref, net.w).data, requires_grad=False)
loss_1 = 255. * criterion(x_pred, img_ref)
loss_2 = 255. * criterion_g(ForwardWeightedGradient().forward(x_pred, net.w), g_ref)
loss = loss_1 + loss_2
loss_history.append(loss.data[0])
print(t, loss.data[0])
# Zero gradients, perform a backward pass, and update the weights.
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm(net.parameters(), args.clip)
optimizer.step()
if it % 5 == 0 and args.log:
writer.add_scalar('loss', loss.data[0], it)
it += 1
if args.save_flag:
base_name = id_generator()
folder_name = args.out_folder
if not os.path.isdir(folder_name):
os.mkdir(folder_name)
fn = folder_name + str(it) + "_" + base_name + "_obs.png"
f = open(fn, 'wb')
w1 = png.Writer(img_obs.size()[2], img_obs.size()[1], greyscale=True)
w1.write(f, np.array(transforms.ToPILImage()(img_obs.data.cpu())))
f.close()
fn = folder_name + str(it) + "_" + base_name + "_den.png"
f_res = open(fn, 'wb')
w1.write(f_res, np.array(transforms.ToPILImage()(x_pred.data.cpu())))
f_res.close()
print("w1 = ", net.w1.data[0])
print("w2 = ", net.w2.data[0])
print("tau = ", net.tau.data[0])
print("theta = ", net.theta.data[0])
print("sigma = ", net.sigma.data[0])
std = 0.1
# Apply noise on chosen image
img_obs = Variable(torch.clamp(GaussianNoiseGenerator().forward(img_ref.data, std), min=0., max=1.)).type(dtype)
lin_ref = ForwardWeightedGradient().forward(img_ref.type(dtype), net.w)
grd_ref = ForwardGradient().forward(img_ref)
img_den = net.forward(img_obs, img_obs).type(dtype)
lin_den = ForwardWeightedGradient()(img_den, net.w)
plt.figure()
n1 = torch.norm(lin_ref, 2, dim=0)
plt.imshow(n1.data.cpu().numpy())
plt.title("Linear operator applied on reference image")
plt.figure()
n2 = torch.norm(grd_ref, 2, dim=0)
plt.imshow(n2.data.cpu().numpy())
plt.title("Gradient operator applied on reference image")
n_w = torch.norm(net.w, 2, dim=0)
plt.figure()
plt.imshow(n_w.data.cpu().numpy())
plt.colorbar()
plt.title("Norm of Weights of Gradient of Noised image")
plt.figure()
plt.imshow(np.array(transforms.ToPILImage()((img_obs.data).cpu())))
plt.colorbar()
plt.title("noised image")
plt.figure()
plt.imshow(np.array(transforms.ToPILImage()((x_pred.data).cpu())))
plt.colorbar()
plt.title("denoised image")
The code (and images as well) is available in its full here.
In the next part of this ticket, I will implement the general form of the aforementionned problem.
You can leave comments down here, or contact me through the contact form of this blog if you have questions or remarks on this post!